一、原理:
贝塞尔曲线于1962年 ,由法国 工程师皮埃尔·贝塞尔 (Pierre
Bézier )所广泛发表,他运用贝塞尔曲线来为汽车 的主体进行设计。贝塞尔曲线最初由 Paul
de Casteljau 于1959年 运用 de
Casteljau 算法 开发,以稳定数值 的方法求出贝塞尔曲线。
线性贝塞尔曲线
给定点 P 0 、P 1 ,线性贝塞尔曲线只是一条两点之间的直线 。这条线由下式给出:
且其等同于线性插值 。
二次方贝塞尔曲线的路径由给定点 P 0 、P 1 、P 2 的函数 B (t ) 追踪:
TrueType 字型就运用了以贝塞尔样条 组成的二次贝塞尔曲线。
![mathbf{B}(t)=mathbf{P}_0(1-t)^3+3mathbf{P}_1t(1-t)^2+3mathbf{P}_2t^2(1-t)+mathbf{P}_3t^3 mbox{ , } t in [0,1]](http://upload.wikimedia.org/math/5/9/7/597ecc5022fa7ab65509d5edfa9c148c.png) 。
。
现代的成象系统,如 PostScript 、Asymptote 和 Metafont ,运用了以贝塞尔样条 组成的三次贝塞尔曲线,用来描绘曲线轮廓。
一般化
P 0 、P 1 、…、P n ,其贝塞尔曲线即
![mathbf{B}(t)=sum_{i=0}^n {nchoose i}mathbf{P}_i(1-t)^{n-i}t^i =mathbf{P}_0(1-t)^n+{nchoose 1}mathbf{P}_1(1-t)^{n-1}t+cdots+mathbf{P}_nt^n mbox{ , } t in [0,1]](http://upload.wikimedia.org/math/5/c/d/5cdbbad5d4698c786a3f02a1b9fb5f2d.png) 。
。
例如 :
![mathbf{B}(t)=mathbf{P}_0(1-t)^5+5mathbf{P}_1t(1-t)^4+10mathbf{P}_2t^2(1-t)^3+10mathbf{P}_3t^3(1-t)^2+5mathbf{P}_4t^4(1-t)+mathbf{P}_5t^5 mbox{ , } t in [0,1]](http://upload.wikimedia.org/math/d/b/4/db41ef611ab1eedb0606d9bce9012c30.png) 。
。
如上公式可如下递归表达: 用  表示由点 P 0 、P 1 、…、P n 所决定的贝塞尔曲线。则
表示由点 P 0 、P 1 、…、P n 所决定的贝塞尔曲线。则
用平常话来说, 阶贝塞尔曲线之间的插值。
又称作 n 阶的 伯恩斯坦基底多项式 ,定义
00 = 1。
点 P i 称作贝塞尔曲线的控制点 。多边形 以带有线 的贝塞尔点连接而成,起始于 P 0 并以 P n终止,称作贝塞尔多边形 (或控制多边形 )。贝塞尔多边形的凸包 (convex
hull)包含有贝塞尔曲线。
为建构二次贝塞尔曲线,可以中介点 Q 0 和 Q 1 作为由 0 至 1 的 t :
- 由 P 0 至 P 1 的连续点 Q 0 ,描述一条线性贝塞尔曲线。
- 由 P 1 至 P 2 的连续点 Q 1 ,描述一条线性贝塞尔曲线。
- 由 Q 0 至 Q 1 的连续点 B (t ),描述一条二次贝塞尔曲线。
 |
![Bezier曲线原理及实现代码(c++) - mappy - mappy 天下 二次贝塞尔曲线演示动画,t in [0,1]](http://upload.wikimedia.org/wikipedia/commons/2/2d/Bezier_2_big.gif) |
|
为建构高阶曲线,便需要相应更多的中介点。对于三次曲线,可由线性贝塞尔曲线描述的中介点 Q 0 、Q 1 、Q 2 ,和由二次曲线描述的点 R 0 、R 1 所建构:
 |
![Bezier曲线原理及实现代码(c++) - mappy - mappy 天下 三次贝塞尔曲线演示动画,t in [0,1]](http://upload.wikimedia.org/wikipedia/commons/f/ff/Bezier_3_big.gif) |
|
对于四次曲线,可由线性贝塞尔曲线描述的中介点 Q 0 、Q 1 、Q 2 、Q 3 ,由二次贝塞尔曲线描述的点 R 0 、R 1 、R 2 ,和由三次贝塞尔曲线描述的点 S 0 、S 1 所建构:
 |
![Bezier曲线原理及实现代码(c++) - mappy - mappy 天下 四次贝塞尔曲线演示动画,t in [0,1]](http://upload.wikimedia.org/wikipedia/commons/7/7d/Bezier_4_big.gif) |
|
P(t)=(1-t)P0 +tP1 , ![]() 。
。
矩阵表示为:
![]() ,
,![]() 。
。
P(t)=(1-t)2 P0 +2t(1-t)P1 +t2 P2 , ![]() 。
。
矩阵表示为:
 ,
,![]() 。
。
P(t)=(1-t)3 P0 +3t(1-t)2 P1 +3t2 (1-t)P2 +t3 P3
矩阵表示为:
 ,
, ![]() 。
。
(6-3-2)
 ,
,![]() 。
。
在(6-3-2)式中,Mn+1 是一个n+1阶矩阵,称为n次Bezier矩阵。
![]() (6-3-3)
(6-3-3)
 。
。
其中,
![]()
利用(6-3-3)式,我们可以得到任意次Bezier矩阵的显式表示,例如4次和5次Bezier矩阵为:
 ,
,

可以证明,n次Bezier矩阵还可以表示为递推的形式:
![]() (6-3-4)
(6-3-4)

二、算法(c++)
工程目录是:Win32App
vc6.0
#include<windows.h>
#include<stdlib.h>
#include<time.h>
#define NUM 10
LRESULT CALLBACK Winproc(HWND,UINT,WPARAM,LPARAM);
int WINAPI WinMain(HINSTANCE hInstance,HINSTANCE hPrevInstanc,LPSTR lpCmdLine,int nShowCmd)
{
MSG msg;
static TCHAR szClassName[] = TEXT(“::Bezier样条计算公式由法国雷诺汽车公司的工程师Pierm Bezier于六十年代提出”);
HWND hwnd;
WNDCLASS wc;
wc.cbClsExtra =0;
wc.cbWndExtra =0;
wc.hbrBackground = (HBRUSH)GetStockObject(WHITE_BRUSH);
wc.hCursor = LoadCursor(NULL,IDC_ARROW);
wc.hIcon = LoadIcon(NULL,IDI_APPLICATION);
wc.hInstance = hInstance;
wc.lpfnWndProc = Winproc;
wc.lpszClassName = szClassName;
wc.lpszMenuName = NULL;
wc.style = CS_HREDRAW|CS_VREDRAW;
if(!RegisterClass(&wc))
{
MessageBox(NULL,TEXT(“注册失败”),TEXT(“警告框”),MB_ICONERROR);
return 0;
}
hwnd = CreateWindow(szClassName,szClassName,
WS_OVERLAPPEDWINDOW,
CW_USEDEFAULT,CW_USEDEFAULT,
CW_USEDEFAULT,CW_USEDEFAULT,
NULL,NULL,hInstance,NULL);
ShowWindow(hwnd,SW_SHOWMAXIMIZED);
UpdateWindow(hwnd);
while(GetMessage(&msg,NULL,0,0))
{
TranslateMessage(&msg);
DispatchMessage(&msg);
}
return msg.wParam;
}
LRESULT CALLBACK Winproc(HWND hwnd,UINT message, WPARAM wparam,LPARAM lparam)
{
PAINTSTRUCT ps;
HDC hdc;
static POINT pt[NUM];
TEXTMETRIC tm;
static int cxClient,cyClient;
HPEN hpen;
int i,j,k,n,t;
switch(message)
{
case WM_CREATE:
static int cxchar;
hdc = GetDC(hwnd);
GetTextMetrics(hdc,&tm);
cxchar = tm.tmAveCharWidth;
ReleaseDC(hwnd,hdc);
case WM_SIZE:
cxClient = LOWORD(lparam);
cyClient = HIWORD(lparam);
return 0;
case WM_PAINT:
hdc = GetDC(hwnd);
srand(time(0));
Rectangle(hdc,0,0,cxClient,cyClient);
for(i=0; i<500; i++)
{
SelectObject(hdc,GetStockObject(WHITE_PEN));
PolyBezier(hdc,pt,NUM);
for(j=0; j<NUM; j++)
{
pt[j].x = rand()%cxClient;
pt[j].y = rand()%cyClient;
}
hpen = CreatePen(PS_INSIDEFRAME,3,RGB(rand()%256,rand()%256,rand()%256));
DeleteObject(SelectObject(hdc,hpen));
PolyBezier(hdc,pt,NUM);
for(k=0; k<50000000;k++);
}
for(i=0; i<100;i++)
{
Ellipse(hdc,rand()%cxClient,rand()%cyClient,rand()%cxClient,rand()%cyClient);
Pie(hdc,j=rand()%cxClient,k=rand()%cyClient,n=rand()%cxClient,t=rand()%cyClient,rand()%cxClient,rand()%cyClient,rand()%cxClient,rand()%cyClient) ;
}
if((n=(n+j)/2)>cxchar*20) n=cxchar*20;
SetTextColor(hdc,RGB(rand()%256,rand()%256,rand()%256));
TextOut(hdc,n/2,(t+k)/2,TEXT(“瑾以此向Pierm Bezier致敬!”),lstrlen(TEXT(“瑾以此向Pierm Bezier致敬!”)));
ReleaseDC(hwnd,hdc);
DeleteObject(hpen);
ValidateRect(hwnd,NULL);
return 0;
case WM_DESTROY:
PostQuitMessage(0);
return 0;
}
return DefWindowProc(hwnd,message,wparam,lparam);
}
版权所有,禁止转载. 如需转载,请先征得博主的同意,并且表明文章出处,否则按侵权处理.

![Bezier曲线原理及实现代码(c++) - mappy - mappy 天下 mathbf{B}(t)=mathbf{P}_0 + (mathbf{P}_1-mathbf{P}_0)t=(1-t)mathbf{P}_0 + tmathbf{P}_1 mbox{ , } t in [0,1]](http://upload.wikimedia.org/math/0/5/c/05c4210c69ffb1358ceb8eb83a1a06fe.png)
![mathbf{B}(t) = (1 - t)^{2}mathbf{P}_0 + 2t(1 - t)mathbf{P}_1 + t^{2}mathbf{P}_2 mbox{ , } t in [0,1]](http://upload.wikimedia.org/math/8/a/d/8adc5cc34ea9649d6e546043fce9c407.png) 。
。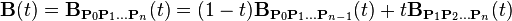
![mathbf{B}(t) = sum_{i=0}^n mathbf{P}_imathbf{b}_{i,n}(t),quad tin[0,1]](http://upload.wikimedia.org/math/3/d/8/3d8f42d9608ecbd44e2f57758d159eb2.png)

![Bezier曲线原理及实现代码(c++) - mappy - mappy 天下 线性贝塞尔曲线演示动画,t in [0,1]](http://upload.wikimedia.org/wikipedia/commons/8/89/Bezier_1_big.gif)





